Konzentrierte Größen in kontinuierlichen Modellen

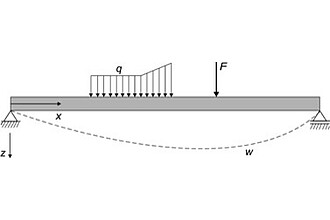
Forschungsgegenstand sind konzentrierte Größen in kontinuierlichen Modellen. Solche konzentrierten Größen können räumlich konzentrierte physikalische Größen sein, wie punktförmig wirkende Kräfte oder zeitlich konzentrierte Größen, z. B. der augenblickliche Kraftstoß bei der Kollision zweier Massen. Betrachtet werden Modelle aus gewöhnlichen Dgln. und Modelle mit verteilten Parametern (partielle Dgln.). Charakteristisch für die Vorgehensweise ist eine der numerischen Integration vorangestellte analytische Integration der Modellgleichung. Sie führt bei zeitlich ausgedehnten impulsförmigen Störungen zu einer Glättung, die für die numerische Integration vorteilhaft ist. Im Grenzfall scharf konzentrierter Größen dient die Deltafunktion als mathematische Beschreibung; sie geht nach der Integration in die sprungartige Thetafunktion (Havyside-Funktion) über, die sich durch ein diskretes Ereignis im Simulationssystem abbilden lässt. Aus partiellen Dgln. der mathematischen Physik entsteht durch sukzessive Zeit-Integration entweder ein System aus zwei partiellen Dgln. (hyperbolische Wellengleichung) oder von partieller Dgl. und algebraischer Gleichung (parabolische Wärmeleitungsgleichung). Die zeitlichen Quellen sind Kraft- oder Wärmeimpulse entlang Saite, Membran und Stab (numerische Integration nach dem Linienverfahren und Visualisierung mit MATLAB) [Publ. 2004]. Es konnte gezeigt werden, dass sich aufgeweichte Punktlasten mittels der Delta-Epsilon-Funktion in Linienlasten zu geschlossenen Ausdrücken der Kraftdichte integrieren lassen. Nach analytischer Integration und Grenzübergang erhält man scharf konzentrierte Punktlasten gemäß der physikalischen Abstraktion (Bild). Die Lösung besitzt eine numerische und eine analytische Komponente [Publ. 2005].